Technical Note 233: IEC651 A-Weight Audio Filtering Software

Technical Note TN-233 Version 1.0

This document describes an implementation of IEC 651 standard A-weight filtering in the form of a downloadable processing command, IEC651A. This processing command runs on a Data Acquisition Processor in the embedded DAPL operating system environment. The problem of measuring apparent sound levels, the role of weighted filtering, and specific use of the IEC651A command for audio analysis are discussed in this note. Finally, information is presented about the limitations of sampled data in general when using the IEC651A command.

Before moving on to the technical details, let's first briefly summarize the key properties of the IEC651A command.

It is compatible with any Data Acquisition Processor product having a 32-bit onboard processor.
It operates upon data streams captured at any sampling frequency in the range 200 to 50000 Hz.
It completely automates filter design. Just tell it the sampling frequency, and it does all the rest.
Depending on Data Acquisition Processor processing capacity, it can analyze a single audio channel or multiple stereo channel sets.
It can work in batch mode for data collection experiments, or in continuous operation.
It conforms to the IEC 651 A-weight reference filter model to within plus or minus 0.1 decibel from 10 Hz through 95% of the Nyquist sampling limit, at any sampling frequency. This improves on the 0.7 dB tolerances for Level 0 instrumentation by almost an order of magnitude, making the command suitable for testing devices intended as Level 0 reference standards.
Because the filter performance is based on numbers, not analog component tolerances, the same filter is equally applicable for less demanding application levels: Level 1 (general laboratory use), Level 2 (general field use) and Level 3 (gross field surveys).
It requires no programming. Define the filtering operation using one line in the DAPL script that configures the data acquisition configuration.
It is the easiest to use. Period. There is no competition.
Oh yes, the price is pretty good too.

Okay, now that we have your attention, let's move on to the technical details.

Accounting for Audibility of Sounds

The problem of measuring audibility of sounds is complicated by the nonlinearity of human hearing. The frequency dependence of human hearing is described by the Fletcher-Munson Curves.

"[The Fletcher-Munson Curve] explains the non-linear response of the human ear , whereby very low and very high frequencies at a given physical intensity are perceived as softer than mid-range frequencies, with 3-4 kHz being the most sensitive frequency range." (Acoustics/Psychoacoustics Theory, Study Guide, Dr. Howard Fredrics, Brown University)

The Fletcher-Munson Curves describe sensitivity to pure tones, but in practice, many sound sources are anything but pure. The apparent loudness of a frequency mix is not necessarily a simple combination of responses to individual frequency bands. To make matters worse, the apparent loudness varies both with the level of the signal and the levels of background noise.

In an attempt to account for human hearing sensitivity in a standardized way so that measurement instruments can be compared, the International Electrotechnical Commission (IEC) issued Standard IEC 651 (1979). This standard identifies four application types (types 0 through 3) and three weighting curve characteristics (A, B and C).

"Owing to the complexity of operation of the human ear, it is not possible at present to design an objective noise measuring apparatus to give results which are absolutely comparable, for all types of noise, with those obtained by subjective methods. However, it is considered essential to standardize an apparatus by which sounds can be measured under closely defined conditions so that results obtained by users of such apparatus are always reproducible within stated tolerances." (IEC 651 1979 - Sound Level Meters)

The A-weighting characteristic is most widely used, and though originally intended for low-level sounds, it is commonly applied to higher sound levels as well.

Applying the A-Weighting Characteristic

For applying the A-weighting curve to a spectral power analysis, one common approach is to first measure the spectral power of a signal under test. The spectrum is partitioned into bands of increasing width, in a geometric sequence. Within each band, the relative contribution to the weighted audio power is adjusted by applying a correction factor based on tables given in the IEC standard. The weighted audio power is then the combination of the weighted contributions from each band.

A variation of this approach can be applied when using FFT techniques for the spectral power analysis. A weighting factor can be computed by integrating the A-weighting curve over the equally-sized frequency intervals spanned by the FFT. The resulting weight-factors are then applied term-by-term to the corresponding terms in the FFT power spectrum. This approach is somewhat awkward, however, because the weighting factors depend on the sampling interval and FFT size. And, of course, this only works in combination with FFT analysis.

An alternative approach is also supported by the IEC specification. The weighting curves are also described in the form of a linear low-order analog filter. Because of its linearity property, the filter adjusts the gain at each frequency but does not shift the signal energy from one frequency band to another, in this manner achieving the desired frequency-dependent weighting. If the original signal is passed through this filter, and then an FFT analysis is applied to the filtered signal, the FFT analysis yields results that are scaled according to the standard weighting curve. The power in the spectrum equals the apparent audio power as defined in the standard.

The IEC651A command is an implementation of the filtering method.

Digitizing an Analog World

An FFT analysis is applied to discrete-time samples of an audio signal. This is inconsistent with a weighting characteristic specified in terms of a continuous-time filter. Either the signal can be filtered first, in the continuous time domain, or the original signal can be sampled first and the filtering performed in the sampled data domain.

While it is possible to build an analog-world filter implementing the standard weighting curve, building a highly accurate one is not a trivial matter. The critical frequencies of the filter range from 26.6 Hz to 12200 Hz, almost three orders of magnitude. The range of component values, component tolerances, drift, parasitic effects, and even the physical packaging make the design and fabrication of the analog filter quite awkward. The difficulty of the task is indicated by the rather huge tolerances the standard allows -- plus or minus 8% in response levels are acceptable for even the highest grade of laboratory filters (Level 0). This is not an attractive alternative.

Digital filtering is much more attractive. The cost of using large or small numbers is the same. The numerical computations can be performed in real time as the signal is digitized, with no need for separate filtering hardware. However, to make this happen, the right digital filter designs must be found. Until now, this alternative has had its own share of problems.

The problem isn't the capabilities of the digital filters. It is how to represent the behaviors of the analog-world filters in the digital-world filters so that the two correspond well in the frequency domain. The usual design techniques for mapping the properties of an analog filter into the equivalent digital filter (impulse-invariant mapping, Tustin's bilinear mapping, Schneider's quadratic mapping, Yule-Walker least-squares fitting, direct rational approximation, etc.) all have limitations. Some techniques work well over part of the frequency range, but then fall apart in the rest of the range. Other methods deliver designs that are accurate but unstable, and therefore useless for real-time filtering.

To understand how some of the problems arise, consider for example the simplest of digital filters, a first-order stage with z-domain characteristic

     Y       a + bz
    ---  =  --------
     U       1 + cz

The frequency response of this expression is obtained by substituting z = exp(j w T) where w is frequency expressed in radians per second and T is the sampling time. The problems arise from the nonlinearity of the exp(j w T) expression and the dependency upon the sampling time T. Change the sampling time, T, and the response changes, in a nonlinear manner. Change the sampling time, and the entire filter stage must be re-designed to obtain an equivalent frequency response at the new sampling rate. The problem just gets more complicated for the case of the more complex A-weight filters.

So what is the solution to this? Simple -- you get somebody else to do the design work. The IEC651A command from Microstar Laboratories provides a complete, integrated, and extremely efficient solution. It combines the best parts of several design methods and integrates them into one automated process.

Using the IEC651A Command

The following example shows a complete DAPL script for a data acquisition configuration. This configuration sends all of the A-weighted data to the PC for logging to a disk. (A PC application program takes care of all of the PC-side data management.)

  ; Data capture and IEC A-weight filtering
  RESET

  ; Configure the sampler for one analog channel
  ; Verify a consistent sampling rate!
  CONSTANT SAMPLING = 44000
  IDEFINE ACQUIRE  1
    SET IP0  S0
    TIME  22.75      ; = 44 kHz rate
  END

  PDEF AWEIGHT
    IEC651A(IPIPE0,SAMPLING,$BINOUT)
  END

  START

The input sampling procedure configured by the IDEFINE command group defines one single-ended analog data channel. Samples are captured at 22.75 microsecond intervals, which corresponds to 44 kHz rates. The processing procedure configures the A-weight filtering for operation at a 44 kHz sampling rate. When the START command is executed, the sampling and processing configurations work together, applying A-weight filtering to the data samples from the input sample pipe, placing the computed results into the $BINOUT binary data channel for transfer to the PC host.

Does it really work? The following configuration substitutes an artificially-generated broad-band noise signal for the signal samples, then computes the FFT spectra of the original noise signal and the filtered version so that they can be compared.

  ; IEC A-weight Filtering Demo
  RESET

  CONSTANT SAMPLING = 22500
  PIPE  POUT, PIN, PR1, PR2
  PIPES SIGSPECT, FILTSPECT, AVSSPECT, AVFSPECT

  PDEF AWEIGHT
    ; No external samples, substitute white noise signal
    RANDOM(0,7171,PR1)
    RANDOM(0,81666,PR2)
    PIN = (PR1-PR2)/2
    ; The A-weight filtering
    IEC651A(PIN,22500,POUT)
    ; Analyze results and send to PC
    FFT32(5,9,0,PIN,SIGSPECT)
    FFT32(5,9,0,POUT,FILTSPECT)
    BAVERAGE(SIGSPECT,256,64,AVSSPECT)
    BAVERAGE(FILTSPECT,256,64,AVFSPECT)
    MERGE(AVSSPECT,AVFSPECT,$BINOUT)
  END

  START

The sampling rate of 22500 Hz yields a Nyquist limit of 11250 Hz in the frequency spectrum, so each 256-term block of FFT spans from 0 through 11250 Hz, roughly half of the audio range. The DAPview for Windows program from Microstar Laboratories was used to display the two spectra.

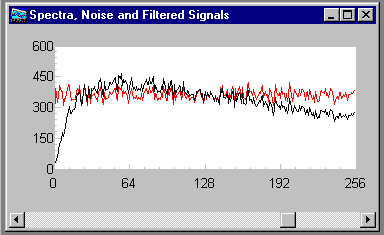
The two spectral plots are obtained by passing the pre-filter and post-filter data streams through FFT processing. The results of analyzing randomized data streams are very noisy, so groups of 64 spectra are averaged.

The results clearly reflect the effects of the A-weighting filter. From a zero-of-transmission at frequency zero, the filter response increases until at 1000 Hz the original spectrum and the filtered spectrum track exactly. This reflects the fact that the A-weight filter characteristic is normalized with 0 dB at 1000 Hz. At approximately 6000 Hz, near the middle of the spectrum plot, there is another crossing of the 0 dB gain level. From there on through the end of the spectrum there is a gradual rolloff. Between 2000 Hz to 4000 Hz there is a small but distinct positive gain. All of these features correspond to the properties of the standard A-weighting curve.

A Word of Warning: Some Practical Hazards!

Suppose you want to measure noise effects in the upper bass to midrange levels. Clearly, there is no need to sample the data at horrendous high rates to capture information about these low frequencies. Also clearly, there is no need to apply IEC A-weight filtering to those octaves that are not relevant. To analyze the frequencies, say, from 0 to 2000 Hz, why not apply the latest Metallica album as a low-frequency noise source, set the sampling rate at 2000 Hz, adjust the IEC651A filter for a 2000 Hz sampling rate, and perform an unhurried FFT analysis on the measurements of the system response?

The most important reason: the measurements are probably invalid.

The choice of Metallica as a test signal is not necessarily so bad. Though plenty heavy in the bass, the biting edge of the distortion generators will provide plenty of harmonics to cover the rest of the audio range. So it is not a lack of spectral information, rather, an overabundance of it that will lead to problems.

Even though the desired information lies in the low portion of the audio spectrum, the digitizer circuits of the Data Acquisition Processor are going to track even the highest frequency components, through the audio range and beyond. For all practical purposes, when it comes time to collect a sample, that sample evaluation is instantaneous. Now suppose the Data Acquisition Processor is tracking a very high frequency waveform, up and down, up and down. Every time as it approaches the top of the fast waveform, the (slow) sampling captures another value. What will the results look like in the data set? The data will be indistinguishable from measurements of a constant offset, a zero-frequency signal. This misrepresentation of a signal at one frequency as a signal at a completely different frequency is a phenomenon known as aliasing.

"After sampling a continuous signal, frequencies above and below the Nyquist frequency (1/2 of the sampling frequency) cannot be distinguished. This is a fundamental limitation of sampled data systems. A signal to be sampled might have frequency components higher than the Nyquist frequency. If so, the effects of these high frequencies on discrete measurements are difficult or impossible to predict, adding or subtracting depending on signal phases.

"Frequencies in bands centered at all multiples of the sampling frequency can corrupt measurements in the low-frequency band. The only way to guarantee good data is to make sure that problem-causing high frequencies are not present in the analog signal when it is sampled." (Internal Microstar Laboratories technical document.)

The solution to avoiding aliasing has two parts. First, pick a sampling frequency at least twice the highest frequency in the band to be measured. That keeps all the desired frequencies below the Nyquist limit. For the case of a 2000 Hz band, the sampling frequency can be no lower than 4000 Hz. Second, make sure that there is no signal energy in frequency bands that might alias onto the desired frequency band. For a 2000 Hz band and 4000 Hz sampling, frequencies in the range from 4000 - 2000 Hz to 4000 + 2000 Hz can corrupt the measurements in the 0 to 2000 Hz range. That leaves no margin between the desired frequencies at the end of the 2000 Hz range and the potentially troublesome frequencies just above. In practice, it is usually better to sample at a higher frequency. For example, with 8000 Hz sampling, frequencies in the range 8000 - 2000 Hz to 8000 + 2000 Hz can affect the measurements in the 2000 Hz band, but what goes on between 2000 Hz and 6000 Hz doesn't matter. It is relatively easy to apply a filter to isolate the 0 to 2000 Hz band from the frequencies 6000 Hz and above.

There are various ways to guarantee that there is no signal energy in the bands at multiples (harmonics) of the sampling frequency.

One way is to use a signal source that is free of the higher-frequencies. (Consider switching from Metallica to an old Michael Bolton album.)
Use an analog filter to screen out the higher frequencies prior to digitizing. (The anti-aliasing filters are much easier to implement than the A-weight filter!)
Apply a complete solution, such as the distortion-free "brick-wall" anti-aliasing filters provided on the Microstar Laboratories iDSC series Data Acquisition Processor boards.
Or apply other anti-aliasing filtering techniques.

Here is an example of how alias- and distortion-free measurements might be obtained in the 0 to 2000 Hz band using a combination of electronic and digital filtering techniques.

Apply a simple resistor-capacitor passive filter that cuts off signal frequencies higher than 20 kHz.
Pass the signal through the analog filter and sample at 40 kHz. The frequency content from 2 kHz through 20 kHz might be corrupted by aliasing from the frequencies between 20 kHz and 38 kHz, but who cares? Only the frequencies below 2 kHz are needed. The filter network cuts off the frequencies 38 kHz and beyond, so no frequency bands will alias onto the important 0 Hz to 2000 Hz band.
Apply the FIRLOWPASS command built into the DAPL operating system, cutting out the higher-frequency information and reducing the effective sampling rate by a factor of 5, to 8 kHz. In the resulting data stream, the Nyquist frequency is at 4 kHz and the data from 0 Hz to 2 kHz is represented perfectly.
FIRLOWPASS(IPIPE0, 5, ANTIALIAS)
Now, apply the IEC651A filter at the sampling rate of 8 kHz. The frequency information for the band from 0 to 2 kHz will be accurate. The frequency band from 2 kHz to the Nyquist limit at 4 kHz is altered by the lowpass filtering and is ignored.

So to summarize, it doesn't make any difference how the high frequencies that lead to aliasing corruptions are removed, just as long as alias effects are not allowed to corrupt the measurements.

Conclusions

Successful A-weighted analysis requires an uncorrupted digitized signal and a good digital filter design. Thanks to the IEC651A processing command, the problems of obtaining a good digital filter are solved. Obtaining a good digitized signal is still a challenge, but no different for A-weight filtering than any other sampled data application.

While not specifically addressing the possibilities, this technical note has suggested that other features built into the DAPL operating system complement the IEC651A filter processing. Among these are

real-time FFT operations,
data averaging,
anti-alias filtering,
direct control of the data acquisition process.

The DAPL system is powerful in its own right, but the IEC651A filtering command extends this power, making high precision audio spectrum analysis easy and cost effective.

Appendix A -- IEC651A

Define a processing task to filter a digitized sample stream in accordance with the IEC-651 (1979) A-weight characteristic.

IEC651A (<inpipe> , <fsample> , <outpipe>)

Parameters

<inpipe>: Pipe containing digitized samples for one audio channel.
WORD PIPE
<fsample>: An integer value specifying the sampling frequency.
WORD CONSTANT
<outpipe>: A pipe receiving the filtered samples.
WORD PIPE

Description

IEC651A defines a processing task that receives samples of a digitized audio signal from pipe <inpipe>, applies A-weight filtering to the data stream, and places the results into pipe<outpipe>. The filter characteristic is fixed, but the representation of the digital equivalent is dependent on the sampling rate, so this information is provided to the task definition by parameter <fsample>. The value of <fsample> can range from 200 through 50000. It affects only the numerical parameters of the digital filter, without affecting runtime complexity.

The filter characteristic conforms to the IEC 651 A-weight reference filter model to within plus or minus 0.1 decibel from 10 Hz through 95% of the Nyquist sampling limit, and within the level 0 tolerance of 0.7 decibels up to the Nyquist limit.

One sample is used to initialize the filter; after that, one output value is generated for each input sample received, preserving the input sampling frequency.

IEC651A filtering applies a frequency-dependent attenuation to the signal. The net weighted power of the output signal can be analyzed by applying the RMS command. Or, a weighted power spectrum can be computed by the FFT32 command.

Examples

IEC651A(IPIPE0, 44000, WPIPE)

Define a processing task that will take a stream of samples digitized at a 44000 Hertz rate (covering the full audio spectrum from 0 through 20000 Hz with a 10% extra margin) from input channel pipe 0 , apply A-weighted filtering, and place the filtered sample stream in user-defined word pipe WPIPE.

IEC651A - A Custom Command for A-Weight Audio Filtering